有兴趣的同学,可以看一看这部分内容,方便工作。 常见的术语比如期望,方差等就不做介绍了,如果这些也要介绍,东西就太多了,这里只介绍一些我自己不是很熟悉的术语及其相关的图形展示,方便记忆和查询。
这部分的内容尽量做到不出现任何公式,通过说人话的方式介绍各个统计学的概念。
四分位数和箱线图
四分位数和箱线图可以方便的展示数据的分布情况。
四分位数
四分位数(Quartile)是统计学中分位数的一种,即把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值就是四分位数。
- 第一四分位数 (Q1),又称“下四分位数”,等于该样本中所有数值由小到大排列后第25%的数字。
- 第二四分位数 (Q2),又称“中位数”,等于该样本中所有数值由小到大排列后第50%的数字。
- 第三四分位数 (Q3),又称“上四分位数”,等于该样本中所有数值由小到大排列后第75%的数字。

第三四分位数与第一四分位数的差距又称四分位距(InterQuartile Range, IQR)。

箱线图(箱形图)
这是一种用作显示一组数据分布的统计图。它能显示出一组数据的最大值、最小值、中位数、下四分位数及上四分位数。箱子中间的线叫做中位线,箱子上下的竖线叫做胡须(whisker),一般情况下,胡须的末端是最大或者最小值。
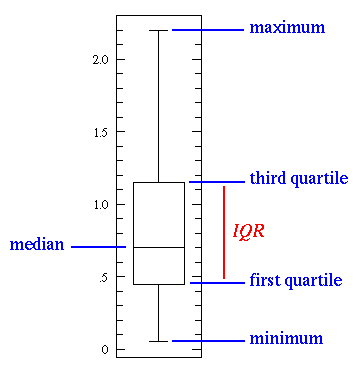
最简单的箱线图展示数据分布的所有范围(最小到最大),可能的变化范围(IQR),典型值(中位数,注意不是平均数)。不正常的值会以异常值的形式分布在最大值和最小值之外。 John Tukey(箱线图发明人)提供了两种异常值的定义:
- 异常值(Outliers):最大值之上或最小值之下3×IQR的数据
- 疑似异常值(Suspected outliers):最大值之上或最小值之下1.5×IQR的数据
如果有上面的任何一种异常值,箱线图的胡须末端为异常值截断点,称为內限(inner fence),位置是Q3+1.5×IQR(和Q1-1.5×IQR),对应疑似异常值用空心圆圈表示。类似的,外限(outer fence)是位于3×IQR处,对应异常值用实心远点表示。
可以发现图的下限并没有到达 Q1-1.5×IQR, 这是因为再往下已经没有数据了, 所以画到这里即可
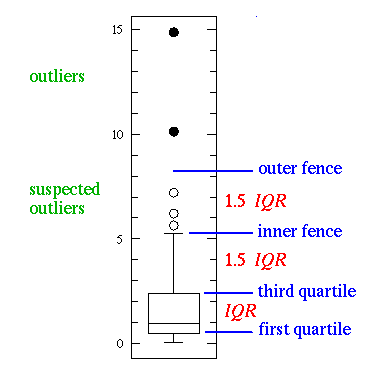
箱线图可以简单理解为: 想象箱子是人的身体, 伸出的线是胳膊. 胳膊有限长度(1.5IQR), 想要包住尽可能多的东西. 如果东西没有那么多, 也没有必要非要伸到最长

相关(correlation)
相关(Correlation,或称相关系数或关联系数),显示两个随机变量之间线性关系的强度和方向。在统计学中,相关的意义是用来衡量两个变量相对于其相互独立的距离。在这个广义的定义下,有许多根据数据特点而定义的用来衡量数据相关的系数。
衡量相关的最常见的方法就是皮尔逊积矩相关系数(英语:Pearson product-moment correlation coefficient,又称作 PPMCC或PCCs, 常用r或Pearson’s r表示),用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。在自然科学领域中,该系数广泛用于度量两个变量之间的相关程度。

几组(x, y)的点集,以及各个点集中x和y之间的相关系数。我们可以发现相关系数反映的是变量线性关系的噪声和相关性的方向(第一排),而不是相关性的斜率(中间),也不是各种非线性关系(第三排)。请注意:中间的图中斜率为0,但相关系数是没有意义的,因为此时变量Y是0。
皮尔逊相关系数的变化范围为-1到1。 系数的值为1意味着X和Y可以很好的由直线方程来描述,所有的数据点都很好的落在一条直线上,且Y随着X的增加而增加。系数的值为−1意味着所有的数据点都落在直线上,且Y随着X的增加而减少。系数的值为0意味着两个变量之间没有线性关系。
相关矩阵
相关矩阵也叫相关系数矩阵,是由矩阵各列间的相关系数构成的。也就是说,相关矩阵第i行第j列的元素是原矩阵第i列和第j列的相关系数。 由于自己和自己的相关就是方差,相关矩阵的对角线就是某组元素的方差,画图中,一般把对角线图形画作此元素的直方图。

T检验
T检验,(Student’s t test, “Student”是笔名),主要用于样本含量较小,总体标准差σ未知的正态分布资料。T检验在零假设基础上,通过比较两组数据,告诉你两组数据是否显著不同。换句话说,T检验告诉你这两组数据的不同是因为巧合还是另有原因。
t检验是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。它与f检验、卡方检验并列。t检验是戈斯特为了观测酿酒质量而发明的。戈斯特在位于都柏林的健力士酿酒厂担任统计学家,基于Claude Guinness聘用从牛津大学和剑桥大学出来的最好的毕业生以将生物化学及统计学应用到健力士工业程序的创新政策。戈斯特于1908年在Biometrika上公布t检验,但因其老板认为其为商业机密而被迫使用笔名(学生)。实际上,跟他合作过的统计学家是知道“学生”的真实身份是戈斯特的。
应用上举例。比如一个药厂研究一款新药,期望可以提高使用者寿命。药厂做了一个实验,召集一些志愿者分为两组,一组服用安慰剂,一组服用新药,最后发现服用安慰剂的组寿命提高2岁,服用新药的组寿命提高3岁。T检验能够告诉你这个提高的区别到底是完全是碰巧的,还是新药真的起了作用。
执行T检验,会有两个结果,一个是t值(t-value),一个是p值(p-value)。
t值越大越大,两组数据不同的可能性越大。
但是t值多大算大呢?我们使用p值来决定。p值得范围从0到1。越小表示越重要,而不是碰巧。一般采用p值0.05来决定是否重要。
零假设
在推论统计学中,零假设或虚无假设(null hypothesis)是做统计检验时的一类假设。零假设的内容一般是希望能证明为错误的假设,或者是需要着重考虑的假设。比如说,在相关性检验中,一般会取“两者之间无关联”作为零假设,而在独立性检验中,一般会取“两者之间是独立”作为零假设。 一般来说,知道证明零假设不成立,零假设都被认为是成立的。统计上记为H0。
与零假设相对的是备择假设(对立假设,alternative hypothesis),即希望证明是正确的另一种可能。从数学上来看,零假设和备择假设的地位是相等的,但是在统计学的实际运用中,常常需要强调一类假设为应当或期望实现的假设。
如果一个统计检验的结果拒绝零假设(结论不支持零假设),而实际上真实的情况属于零假设,那么称这个检验犯了第一类错误。反之,如果检验结果支持零假设,而实际上真实的情况属于备择假设,那么称这个检验犯了第二类错误。通常的做法是,在保持第一类错误出现的机会在某个特定水平上的时候(即显著性差异值或α值),尽量减少第二类错误出现的概率。
